並べ方 と 組み合わせ 方 問題

オレンジ と 黒 の 蛇小6算数「ならべ方と組み合わせ方」学習プリント・練習問題 . 小6算数「並べ方と組み合わせ方」の文章問題プリント(難しい) 小学6年生算数で習う並べ方と組み合わせ方の文章問題プリントです。 並べ方では、色のぬり分け、組み合 …. 小学6年生の算数 【場合の数・順列】 練習問題プリン …. 組み合わせ方、並べ方を、落ちや重なりがないように順序よく整理して、調べる方法を練習できる問題プリントです。. 場合の数・順列（1）. 答え. 場合の数・順列（2）. 答え. 場合の数・順列（3）. 答え. 場合の数・順列（4）. 答え. 「ならべ方」と「組み合わせ」｜小学校の「場合の数」の問題 . 並べ方と組み合わせ方のプリント. 並べ方と組み合わせ方のプリント. 並べ方と組み合わせ方の練習問題プリントです。. 小学校6年生の算数で学習する単元で文章問題を読みながら樹形図を …. 【すきるまドリル】 小学6年生 算数 「場合の数」 無 …. 並び方や違いに気づき、順序よく道筋を立てましょう。 目的に応じた道順を考え、落ちや重なりがないように考えましょう。 プリント一覧. 場合の数 ①. 場合の数 ③. 場合の数 ④. ☆プリントの答え☆. 関連する学習プリント. 【すきるまドリル】小学4年 漢字ワーク「 …. 世界一分かりやすい算数 小6 「場合を順序よく整理し …. 『 世界一わかりやすい算数問題集シリーズ』の小6算数 「場合を順序よく整理して」です。例題、練習問題、まとめテストがついています。これを使って満点目指して頑張ってください！すべて無料でダウンロードできるので、学校や塾、家庭教師、ご自宅等でご自由にお使いくだ …. 場合の数 組み合わせ | 無料で使える学習ドリル. ホーム. 算数・計算. 場合の数 組み合わせ. エクセル 半分 に 分ける

住友 生命 ふる はーと 評判場合の数の組み合わせの問題です。 並べ方 との違いを次の文章から読み取れるようにしてください。 A,B,Cの3人から2人選んで並べる. 1番目と2番目の区別をつけて並べます。 6通りになります。 A,B,Cの3人から2人選ぶ. 上の ….

【小6算数】「並べ方と組合せ方」の問題 どこよりも …. 「並べ方」は直線で結ぶ図で求めましょう「組合せ方」は直線で結ぶ図、表を作る、図形を使う方法で求めましょう 慣れてきたら図を一部書いてから「計算で求める」こともできるようになりますよ. 6年算数 並べ方と組み合わせ方(場合の数)の教え方. ①図や表を使って、 順序よく整理 する方法 ②図や表を使って、全部の中から 条件にあった組み合わせや並べ方 の見つけ方 ③ 組み合わせや並べ方 を整理して、 落ちや重なりがない 調べ方 ④いろいろな場合を考えて、 場合をあげて調べ条件 にあうもののみつけ方. ※このページは場 …. 順列と組み合わせの公式とその違い【問題付き】 - 理 …. 並べる→順列、並べない→組み合わせはわかるのですが、 いざ問題を解こうとしたとき、 順列か組み合わせか、樹形図を使うのか、判断がつきません。. 場合の数（組み合わせ）の問題一覧 | 中学受験の算数 …. PR. 場合の数（組み合わせ）の問題一覧. ヘクトパスカル最新の動画. ちょっと高度なシニアの算数講座 (N.157)｜【淑徳与野中学】 ＜言われればアーそうか！ という図形の問題です。 ＞毎回の宿題を，次回の動画で解説。 毎週（火）（金）配信小学生からお年寄りま …. 【3分で分かる！】順列と組み合わせの違いと公式をわかり . 順列とは、いくつかのものを順序をつけて列に並べる 並べ方 の総数です。 組み合わせとは、いくつかの要素の集まりからいくつかの要素を選び出すとき …. 6年算数「並べ方と組み合わせ方(場合の数)」並べ方の教え方. ①図や表を使って、 順序よく整理 する方法 ②図や表を使って、全部の中から 条件にあった組み合わせや並べ方 の見つけ方 ③ 組み合わせや並べ方 を整理して、 落ちや重 …. 小学校6年生の「並べ方と組み合わせ（場合の数）」 - 小学生 . 小学校6年生の「並べ方と組み合わせ（場合の数）」 - 小学生の無料算数プリント「ふたば問題集」 算数プリント解説ブログ. 小学校6年生の「並べ方と組み …. 組み合わせの応用問題 | Study-Ant. 組み合わせの応用問題. 組み合わせ. 重複組み合わせ. はじめに. 前回学んだ組み合わせの計算には，様々な活用方法があります。 色々な応用問題を確認してみましょう。 …. 並べ方と組み合わせ方-その1 | 家庭学習レシピ. 2015年3月10日 2022年4月1日. 並べ方と組み合わせ方についての家庭学習をしてみましょう。 樹形図、表、そして辺と対角線の数で考えるなど、組み合わせ方を調べるの …. 「組み合わせ」の問題パターンと解き方を解説（中学入試対策）. 組合せ…順番を区別しない. 並べ方…順番を区別する. 1，2，3の3枚のカードから2枚を選ぶときで考えてみます。. 組合せ…1と2、1と3、2と3の3通り. 並べ方…1→2、1→3 …. 場合の数 順列と組み合わせの違いと並べ方問題の解き方. 順列と組み合わせは基本的な見分け方は簡単ですが、問題のパターンも多いので少し時間が必要な単元だと覚悟した方が良いです。 先ずは順列、並べ方の …. 小6算数 【並べ方・組み合わせ】超簡単な解き方あり . - YouTube. 小学生の6年生（小6）が勉強する【並べ方・組み合わせ方】を元小学校の先生がオンライン授業します。 ①並ぶ順番②4つの数字から2桁を作る③コイン …. 並べ方と組み合わせ アーカイブ - 小学生の無料算数プリント . 並べ方と組み合わせ アーカイブ - 小学生の無料算数プリント「ふたば問題集」 6年生・学習のポイント. 小学校6年生の「並べ方と組み合わせ（場合の数）」 この章では、 …. 並べ方と組み合わせ方【お金を組み合わせてできる金額】小6算数. Tweet. 並べ方と組み合わせ方について最初から復習したい生徒さんや、はじめて学習する6年生にぴったりの教材！ 4種類の硬貨から2つを選んだときの金額を調べる学習 …. 小学6年生の算数 【場合の数｜組み合わせ】 練習問題プリント . 順序は考えず選んで組を作るときの選び方 「組み合わせ」を調べる方法を練習できる問題プリントです。 場合の数・組み合わせ（1） 答え. 場合の数・組み合わせ（2） 答 …. 第6学年 算数科 「並べ方と組み合わせ方」 （全6時間 . 1. ・簡略化. 第6学年 算数科 「並べ方と組み合わせ方」 （全6時間）. 「順序よく整理して調べよう」（東京書籍・6年）. ・具体的な事柄について、起こり得る場合を順序 …. 複雑な並べ方と組み合わせ｜問題の考え方と解き方. ＜複雑な並べ方と組み合わせ-2 ＞（上の問題と類似 ※(3)は難 ） 白石が2個と黒石が5個あります。 この7個のご石を横1列に並べるとき，次の問いに答えな …. コース立方体組み合わせテスト｜はらリハ【自費リハビリ&脳 . はじめに コース立方体組み合わせテストは『知能指数：IQ』を評価する神経心理学検査の1つです。 言葉の理解や表出が難しい失語症の方に対しても行うことが可能 …. 遠隔接客や画像認識AI、人手補う無人・省力化技術を競う - 日本 . 次世代の店舗や街づくりに関する製品・技術を集めた総合展示会「日経メッセ 街づくり・店づくり総合展」が12日から15日まで、東京ビッグ . Apple、モルガン・スタンレーが導入する「すごい会議」はなぜ . AppleやAdobe、モルガン・スタンレーなど、世界の名だたる大企業が導入する「すごい会議」とはいったいどんなものか。その手法やうまくいく企業 . 並べ方と組み合わせ方【お金を組み合わせてできる金額】小6算数. 4種類の硬貨から2つを選んだときの金額を調べる学習プリントです。. 【並べ方と組み合わせ方6】2つ選ぶ組み合わせ（樹形図） のプリントと同じように樹形図をかいて求めます。. 実際に硬貨を並べてみるとよりイメージしやすくなるかもしれませんね . 【並べ方と組み合わせ方6】2つ選ぶ組み合わせ（樹形図）. 4種類から2つを選ぶ組み合わせを、樹形図をかいて調べます。 確認までは4つ、定着からは5つから2つを選ぶ問題になります。 一度すべての組み合わせを書いてから重複分を消すやり方にしています。 重複分を減らしながら組み合わせを書いていくのは少し難しいのでまずはこのやり方で挑戦し . 【SPI対策】「順列・組み合わせ(場合の数)」の練習 …. この記事では、SPIの「順列・組み合わせ」の練習問題や解き方のコツについて解説します。 あわせて、SPIの順列・組み合わせに使う公式や対策方法を紹介しているのでぜひ参考にしてみてください。 ちなみに、 「SPI …. 6年算数「並べ方と組み合わせ方(場合の数)」並べ方の教え方. 出典：「算数教科書の用語・記号教え方ガイドブック」より 明治図書）.

【場合の数】. 与えられた何種類かのものを、組み合わせたり、順序よく並べたりするときに、考えられるだけの並べ方、あるいは、組み合わせ方が何通りできるかを数える。. 日焼け 止め ジェル と ミルク 違い

手 の シミ 取りその数 . 「組み合わせが何通りあるのか」の求め方を解説（表と図で . 組み合わせを表で表して調べてみよう 「並び方が何通りあるか」の学習では、4つの数字を並べたときに何通りの並べ方があるかなどを表や図であらわして調べたね。 こんどは、数字などを選ぶときに、「組み合わせは何通りあるか」を表や図をつかってあらわす方法を考えていくよ。. 並べ方と組み合わせ アーカイブ - 小学生の無料算数プリント . 小学校6年生の「並べ方と組み合わせ（場合の数）」. この章では、起こりえるすべての場合を適切に分類整理して、順序よく並べることをねらいとしています。. 不安なところ、つまづきやすい所はふたば問題集の無料プリントでくりかえし学習するのがお . 6年生算数「並べ方と組み合わせ」 - YouTube. 6年生算数の並べ方と組み合わせです。動画の最中に右上にカードを出しますので、その都度動画を止めて、そこに書かれた問題を解きながら …. 並べ方と組み合わせ方の違いとは？ 順列と組合せを区別して . 多くの中学受験生が算数でつまずく単元は「場合の数」です。中でも、並べ方と組み合わせ方の違いで混乱する受験生が続出します。これらの違いをしっかり言葉で理解し、パターン暗記に頼らずに問題を解けるようにすることが大切です。. ツイン タワー すみ とし 住吉 館

pc 起動 しない ファン 回る

小学6年生の算数プリント問題集 - ふたば問題集. 対称な図形、分数と整数のかけ算・わり算、円の面積、文字を使った式、データの活用、角柱と円柱の体積、分数のかけ算、分数のわり算、並べ方と組み合わせ（場合の数）、比、拡大図と縮図、比例と反比例、およその面積や体積. 並べ方と組み合わせ方【試合の対戦表をつくろう】小6算数｜無料. 九九と表と同じように、同じ対戦になる組み合わせがあることに注意しましょう。. 樹形図でも求められますが、重複した分を消さなければいけないのが少し難しいです。. このやり方でなくても間違えずに答えを求められればOKです！. まとめPDF「【並べ方 . 順列と組み合わせの違いと見分け方！公式や練習問題 | 受験辞典. 「順番に並べる」「順番を変えると意味が変わる」ときは順列になります。 反対に、「順番に並べない」「順番を変えても意味が変わらない」ときは組み合わせになります。 例題を通して見分け方を身につけましょう。 例題①「3 . 並べ方と組み合わせ まとめの問題 - 小学生の無料算数プリン …. 2 答えは10～14ページ 第9章 並べ方と組み合わせ まとめの問題 あかりさん，しょうさん，たかひろさん，なおさん，ゆうきさんの 5人が総当たりの対戦を行います。 5人が対戦する組み合わせは全部で何通りですか。 表と裏の区別がつくコインを3回投げます。. 〈6年算数 順序よく整理しよう！②〉 「組み合わせ方」はこれ . 「並べ方」「組み合わせ方」のちがいは分かるかな？どちらも図や表を使って解いていきますが、全く同じやり方というわけではありません . 「並べ方が何通りあるのか」を求める問題の解き方をわかり . 小学校6年生算数で学習する「並べ方が何通りあるのか」を求める問題のタイプごとに解き方をわかりやすく解説。数字4桁の並べ方を求める問題、2つの数字を選んで並べ方を求める問題、コインの裏と表の並べ方を求める問題など。. 前田の算数「場合の数」おすすめ問題5 - plala.or.jp. 6年 「場合の数」. 「場合の数」の単元には、面白い問題がたくさんある。. その中でも、私が特に気に入ってる問題を5つ紹介したい。. 階段の上り方は、何通り？.

いろいろな発想が出てくる！. 階段の上り方は何通り？. 鶯 とろ

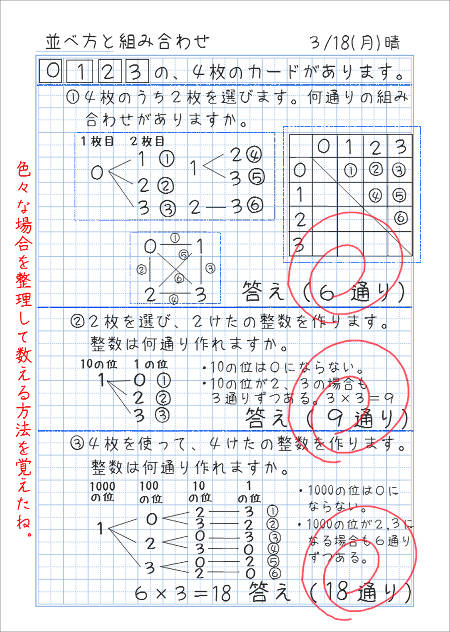
琉 ちゃ ろ ハゲ条件② 1段か2段ずつ上る。. 「場合 . 小学6年生「算数」学習プリント・問題集 | 無料ダウンロード印刷. 小学6年生算数で習う「並べ方と組み合わせ方」「場合の数」の学習プリント(練習問題・テスト・ワークシートドリル)です。 順序よく整理して調べようの単元では、何通りのならべ方や組み合わせ方があるのか、計算や樹形図、表を使い. スマホOK!【6年】並べ方と組み合わせ方（場合の数）〜 並べ方 . 並べ方を考える時には、図や表を使って順序よく調べると、「落ち」や「重なり」がないように調べることができます。特に樹形図がオススメ . 並べ方と組み合わせ方-その2 | 家庭学習レシピ. 2015年3月11日 2022年4月1日 今日は、並べ方と組み合わせ方の、もう1つのノート例を紹介します。 並べ方と組み合わせ方の練習問題 組み合わせ方について、これよりもう少し基本的な学習内容のノート例です。よろしければ、こちらもご覧下さい。. 場合の数・順列 (1) - ちびむすドリル. baainokazu. 【場合の数】. あることがらについて、そ の起こり方が何通りあるか調べることを、場 合の数を求めるといいます。. 【順列】. いくつかのものを順番に並べるときの並べ方を順列といいます。. 【順列の場合の数の求め方】. 順列の場合の数の求め . 【6年算数】並べ方、組み合わせ【授業アイディア・ネタ . 6年算数、組み合わせの授業です。自分たちの身近なものに教科書の問題を置き換えるだけでも子ども達の意欲は高まります。並べ方や組み合わせの導入段階での授業アイディアです。 サンバ先生の 明日使える教育実践 Home Profile . 小学校で扱う場合の数の組み合わせの考え方 | みけねこ小学校. 順列(並べ方)とはまた違った数え方をしないといけない組み合わせ。 うまく数えるコツをつかめるととても楽に問題を解くことが出来る単元になります。 今回の記事では、組み合わせの数の数え方について書いてみたいと思います。. 6年算数「並べ方と組み合わせ方(場合の数)」並べ方の教え方. 出典：「算数教科書の用語・記号教え方ガイドブック」より 明治図書）. 【場合の数】. 与えられた何種類かのものを、組み合わせたり、順序よく並べたりするときに、考えられるだけの並べ方、あるいは、組み合わせ方が何通りできるかを数える。. その数 . 特 養 に 早く 入れる 方法

ぐっすり ず む 副作用指導案「並べ方と組み合わせ方」 - 珠洲たのしい授業の会. 指導案「並べ方と組み合わせ方」. 2022.07.17. 「順列・組み合わせ」を扱う小学生版の単元です。. こういう単元が小学生に本当に必要なのかどうかは，あまり深く考えたことはありません。. 賃貸 床 剥がれ た

旋盤 で 作れる もの中高へ進むと「全部で何種類あるのか」なんて簡単な計算ででき . スマホOK!【6年】並べ方と組み合わせ方（場合の数 . - YouTube. 組み合わせ方では、図や表を使って重なりに注意しながら調べていくことが大切になります。様々な図や表を使い分けて、自分のやりやすい方法 . 順列とは？理解しておきたい4つの公式と計算方法 | HEADBOOST. 1. 順列とは 順列とは「n 個の異なる物の中から r 個を取り出して順番に並べた時の、並べ方の全パターンの数」のことです。 たとえば A, B, C の 3 つの異なる記号から 2 個取り出して順番に並べるとします。この時にありうるパターンを全て書き出して見ると、以下の樹形図で示してい …. 乾杯 の ご 発声 依頼

痔 の 診察 恥ずかしい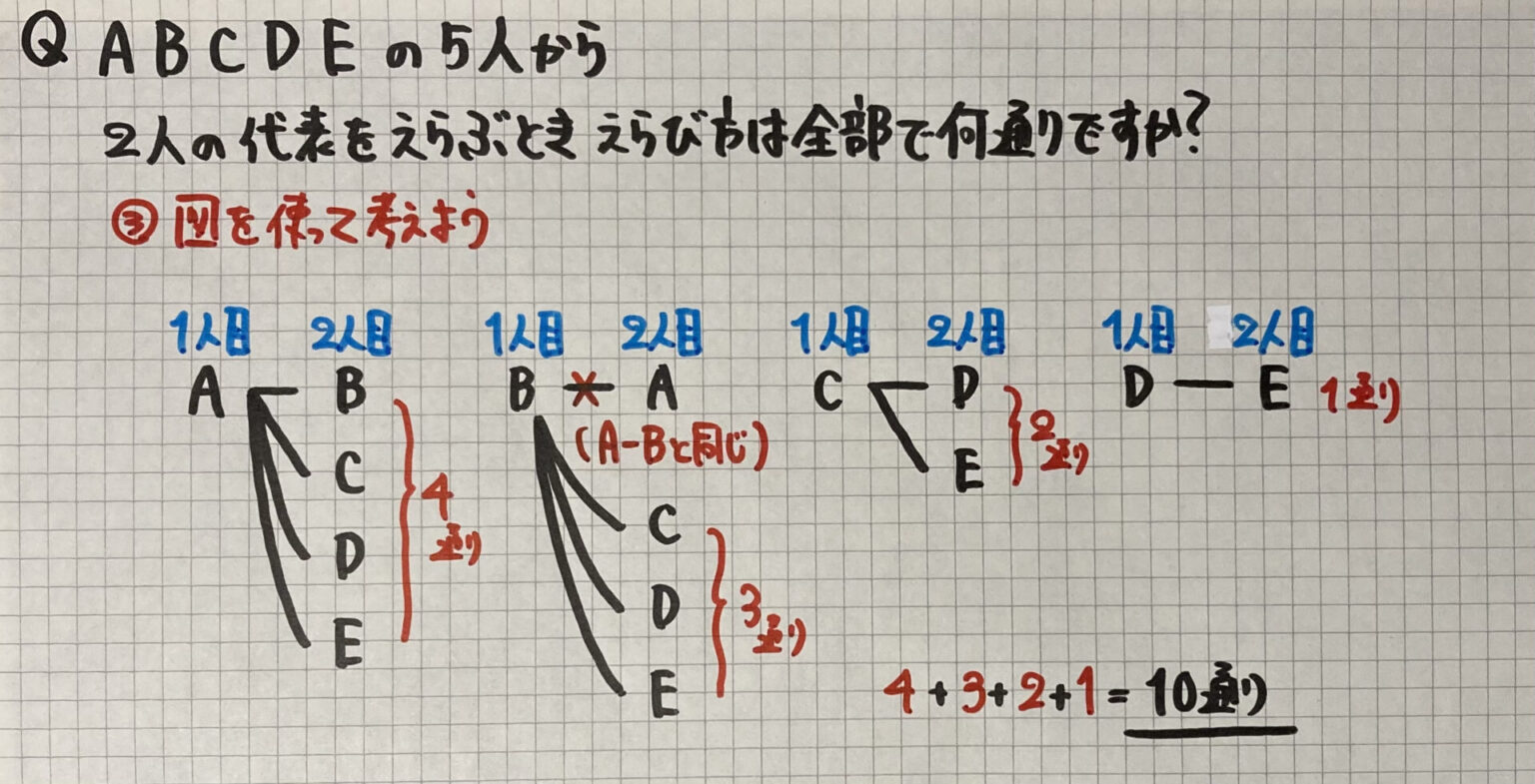

算数科学習指導案 - 国立大学法人 北海道教育大学. 算数科学習指導案 1．単元名「並べ方と組み合わせ方」 2．単元の目標 起こり得る場合を考える際に，事象の特徴に着目し，落ちや重なりなく調べる方法を考察するなどの数学 的活動を通して，図や表などにかき表したりするよさを理解するとともに順序よく整理して調べることがで. 複雑な並べ方と組み合わせ｜問題の考え方と解き方 | 中学受験 . ＜複雑な並べ方と組み合わせ-2 ＞（上の問題と類似 ※(3)は難 ） 白石が2個と黒石が5個あります。この7個のご石を横1列に並べるとき，次の問いに答えなさい。 （1）白石2個がとなりあっている並べ方は，全部で何通りありますか。. 【高校数A】『順列・組み合わせ』の頻出問題を元数学科が解説 . 今回は【高校数学】【数A】『場合の数と確率』から組み合わせについて、基礎を徹底解説しました。組み合わせの定義から重複組み合わせについての紹介・証明をして、それぞれの項目で練習問題を用意しました。苦手な方でもわかりやすくしたつもりですのでぜひご覧ください。. 花まるワーク6年後期 - 教育出版. 単元12 並べ方と組み合わせ PDF 692KB 単元12 並べ方と組み合わせ 解答 PDF 694KB 6年後期一括ダウンロード ワークシート PDF 2.0MB 解答 PDF 2.1MB PDFファイルは，クリックすると内容を別ウィンドウに表示します。 …. 問題のアレンジ力～スモールステップから発展問題まで～. 第6学年算数「並べ方と組み合わせ方」の単元において 上越市立大潟町小学校 教諭 野口 正行 1 目指した子どもの姿 複雑な問題が出てきても、自ら「足場」をつくり、かかわって問題を解く子どもを目 指す。. 数学のPやCってナニ？並べ方や組合せを高校生がわかりやすく . 問題作成上、1人がはぶられてしまっていますが、あまり気にしないこと。 さて、この例題1は、4種類の人間が1人ずついるとき、3人を取った後の並べ方を求める問題です。（人を軽んじたような冷たい表現ですが、あくまでわかりやすく説明するための表現です）. 小学校で扱う場合の数の組み合わせの考え方 | みけね …. 順列(並べ方)とはまた違った数え方をしないといけない組み合わせ。 うまく数えるコツをつかめるととても楽に問題を解くことが出来る単元になります。 今回の記事では、組み合わせの数の数え方について書いてみたいと思います。. 順列とは？理解しておきたい4つの公式と計算方法 | HEADBOOST. 1.

順列とは 順列とは「n 個の異なる物の中から r 個を取り出して順番に並べた時の、並べ方の全パターンの数」のことです。 たとえば A, B, C の 3 つの異なる記号から 2 個取り出して順番に並べるとします。この時にありうるパターンを全て書き出して見ると、以下の樹形図で示しているように 6 . 場合の数〔ならび方や組み合わせ方を調べよう〕（第6学年 . 1問目の問題の考え方からの違いに着目させ、数字の組み合わせだけでなく、組み合わせた後に、ならび方を考える必要があるということに着目させたかったためである。この問題についても、児童はデジタル教科書の機能を使って、考えて. 指導案「並べ方と組み合わせ方」 - 珠洲たのしい授業の会. 指導案「並べ方と組み合わせ方」. 2022.07.17. 「順列・組み合わせ」を扱う小学生版の単元です。. いとこ の 旦那 呼び 方

顎 の 付け根 が 痛いこういう単元が小学生に本当に必要なのかどうかは，あまり深く考えたことはありません。. 中高へ進むと「全部で何種類あるのか」なんて簡単な計算ででき . 組み合わせの考え方と公式（組み分けと道順を求める問題の . 組み合わせの考え方は順列と同じ手順をとれば簡単です。 計算公式もありますが、公式で求まるのは部分的な計算だけなので公式を使うことが目的ではありません。 組み分けと道順の数を求める問題を説明しますが、計算方法ではなく考え方 …. 場合の数・順列 (1) - ちびむすドリル. いくつかのものを順番に並べるときの並べ方を順列といいます。【順列の場合の数の求め方】 順列の場合の数の求め方には、計算で求める方法や、樹形図をかく方法などがあります。abcの順にかくなど、ルールを決めてかくと、 【樹形図の. 6年算数「並べ方と組み合わせ方(場合の数)」並べ方の教え方. 出典：「算数教科書の用語・記号教え方ガイドブック」より 明治図書）. 【場合の数】. 与えられた何種類かのものを、組み合わせたり、順序よく並べたりするときに、考えられるだけの並べ方、あるいは、組み合わせ方が何通りできるかを数える。. その数 . 【基本】組合せ | なかけんの数学ノート. 【基本】順列で見たように、「順列」は選んだ後に並べましたね。ここで考えるのは、選ぶだけです。順番は気にしません。 例えば、もし問題が「1列に並べる」となっていれば、次の3つの並べ方は「別物」とカウントします。 1. 順列と組み合わせ(場合の数と確率)｜高校数学のつまずきやすい . 高校生の勉強方法 スタッフ管理 順列と組み合わせ(場合の数と確率)｜高校数学のつまずきやすい単元を徹底解説！ 数学が苦手なお子さんの数は中学、高校とも学年が上がっていくごとに増えていきますよね。特に中学から高校に上がって高校1年生から分からなくなってしまう人が多いです。. 【SPI】組み合わせと順列の練習問題まとめ＆詳しい解説付き. SPIの非言語（数学）では組み合わせと順列に関する問題が頻出なので、SPIで高得点を狙っている就活生・転職活動中の社会人は必ず対策しておくべきです。. ※「 SPIの非言語（数学）を完全解説！. 対策方法やできない人でも点数を上げる方法！. …. 「並べ方が何通りあるのか」の求め方を解説（表と図での表し . 小学校6年生の算数で学習する「並べ方」について、並べ方が何通りあるのかを求める方法をわかりやすく解説。「表」を使って並べ方が何通りあるかを求める方法、「図」を使って求める方法、それぞれのやり方をくわしく紹介。. 算数科学習指導案 - 国立大学法人 北海道教育大学. 算数科学習指導案 1．単元名「並べ方と組み合わせ方」 2．単元の目標 起こり得る場合を考える際に，事象の特徴に着目し，落ちや重なりなく調べる方法を考察するなどの数学 的活動を通して，図や表などにかき表したりするよさを理解するとともに順序よく整理して調べることがで. 組み合わせ＝並べない順列のこと。考え方と計算方法を解説 . 組み合わせとは 「並べない順列」というのも少し日本語がおかしいですが、つまり組み合わせとは「選ぶだけ」の場合の数の事を言うんです。 たとえば順列が「7個のボール中から→3個選んで→1列に並べる」という場合の数を数えたのに対し、組み合わせは「7個のボールの中から→3個を選ぶ . 順列と組み合わせの数の公式。どちらを使うのが正しいか迷っ . この2種類の問題では、それぞれ答えが変わってきます。 ①は順列で、答えは 5 P 2 ＝5×4＝20通り ②は組み合わせで、答えは 5 C 2 ＝5×4÷2＝10通りになります。 今回は、そんな順列と組み合わせの数の考え方についてです。. SPI 『順列・組合せ（場合の数）』 ～練習問題と解き方を徹底 . SPIの『順列・組合せ』の練習問題一覧と問題の解き方を、どんな書籍やどこのサイトよりも詳しく解説しています。『順列・組合せ』の問題を解くには、順列を求める公式と、組み合わせ数を求める公式の2つを知っている必要があります。公式の使い方なども解説しているので、是非、ご活用 . Pythonで順列と組み合わせ #Python - Qiita. Pythonでは、順列、組み合わせとかを本当に直感的に表示・計算出来て便利。 参考 ここの内容で全て事足りました。 順列 (P:Permutations) a,b,c,d,e 5つの要素が会った時の並べ方のパターンは、5!（5の階乗個）。つまり、. 算数 6 - 学校図書株式会社. 並べ方と組み合わせ方の適用問題 を解く。 観点を確認しながら指導し，必要に 応じて前に戻り復習する。6－5 2 文字と式 文字を使って量や関係を式に表そう ＜ 4 月下旬～5 月中旬・12ページ・8時間＞ 学習指導要領との関連 A(2) 評価 . 〈6年算数 順序よく整理しよう！③〉「並べ方」 「組み合わせ . 「並べ方」「組み合わせ方」の入試問題編です！これまでの問題よりさらにレベルアップしていますが、今回できなくてもまたやり直してできる . 【小6 算数】 小6－39 組み合わせ方 - YouTube. 【他の動画の一覧表はブログからお願いします】ブログはこちらから → meblo.jp/katekyo-children/古い動画なので . 円順列の公式と2通りの考え方 | 高校数学の美しい物語. 円順列に似たものとして 数珠順列 というものもあります。 円順列では「回転して一致するものは同じ並べ方」とみなしました。 数珠順列では 「回転または裏返しで一致するものは同じ並べ方」 とみなします。 図のような2つの並べ方は「同じ」とみなします。. 中学受験 場合の数 まとめの問題 | 中学受験準備のための学習 .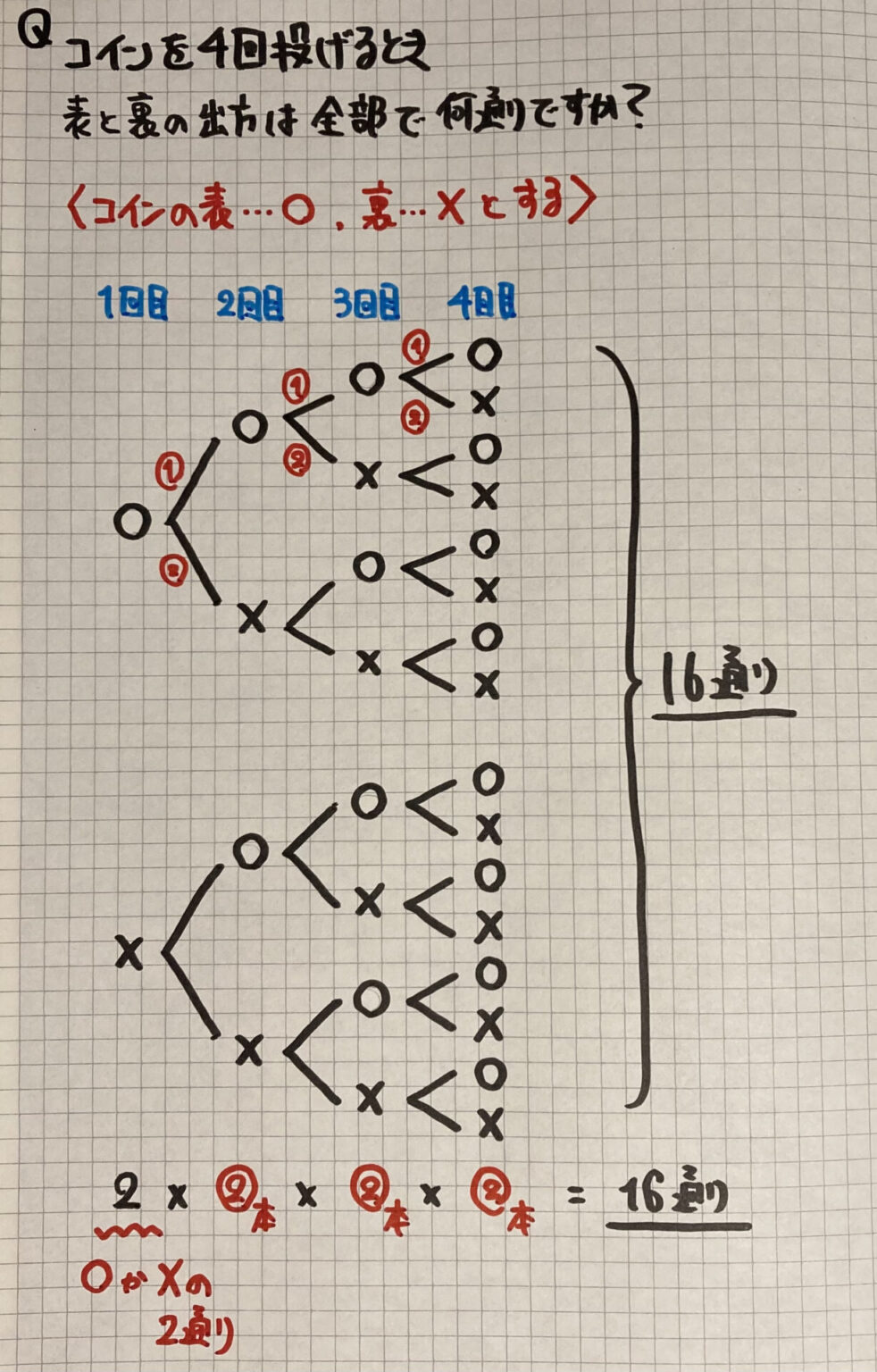

中学入試問題の中から場合の数の問題や類題をピックアップした練習問題プリントです。 基本的な小問が中心となりますので、模擬試験や入試前の復習問題としてご利用ください。学習のポイント 場合の数の問題は 並べ方や組み合わせを書き出す ことが基本になります。. 【高校数A】『順列・組み合わせ』の頻出問題を元数学科が解説 . 今回は【高校数学】【数A】『場合の数と確率』から組み合わせについて、基礎を徹底解説しました。. 組み合わせの定義から重複組み合わせについての紹介・証明をして、それぞれの項目で練習問題を用意しました。. 苦手な方でもわかりやすくした …. 円順列の応用問題5選+難問2選を解説【順列との違いとは . 補集合の考え方は応用範囲が非常に広いので、ぜひ押さえておきましょう。. 選んで並べる問題. 問題. 弔電 と 香典

特別 児童 扶養 手当 b2 もらえ た生徒 $9$ 人のうち $5$ 人を選んで輪の形に並べる場合の数を求めよ。. 一見難しくなさそうですが、今までにない発想が必要です。. 【解答】. 「選ぶ」と . 複雑な並べ方と組み合わせ｜問題の考え方と解き方 | 中学受験 . ＜複雑な並べ方と組み合わせ-2 ＞（上の問題と類似 ※(3)は難 ） 白石が2個と黒石が5個あります。この7個のご石を横1列に並べるとき，次の問いに答えなさい。 （1）白石2個がとなりあっている並べ方は，全部で何通りありますか。. 【東書Eネット】【6年⑪】組み合わせ ～順列と組み合わせの . 2020～2023（令和2～5）年度用教科書「新しい算数6」に準拠。（math connect「今日の授業のひと工夫」）この単元では、「順列（並べ方）」と「組み合わせ」を学習します。これらはそれぞれ独立したものではなく、関連性があり . 【小6 算数】 小6－37 並べ方① - YouTube. 【他の動画の一覧表はブログからお願いします】ブログはこちらから → meblo.jp/katekyo-children/古い動画なので . 条件整理と場合の数 問題一覧 | 中学受験の算数・理科 . 複雑な並べ方と組み合わせ 図形と場合の数 ルールの問題 推理の問題 投票の問題 階段の上がり方 きまりを見つけて解く問題（おまけで1本もらえる問題） 5年上第11回「場合の数-ならべ方-」例題一覧. 場合の数 並べ方の問題 | 中学受験準備のための学習ドリル. 練習問題をダウンロードする. 画像をクリックするとPDFファイルをダウンロードできます。. 問題は追加する予定です。. 場合の数の順序を考えに入れた並べ方（順列）の問題です。. もれや重なりのないよう、順序よく図に表した樹形図を書いて …. 腐っ た ピーマン

重複組合せ( {}_nH_r) とは？公式と具体例を解説【整数解問題 . 数学A「場合の数」の発展事項として登場する「重複組合せ」。 重複組合せの公式は少しとっつきにくいので、苦手意識を持っている方もいると思います。 でもその本質は〇と仕切りの並べ方を考えているだけ！ この仕組みが理解できていれば、公式を覚える必要もありません。.